Finite State Machines
Motivation
State machines can be used in a diverse range of scenarios such as
Explaining why you are a procrastinator
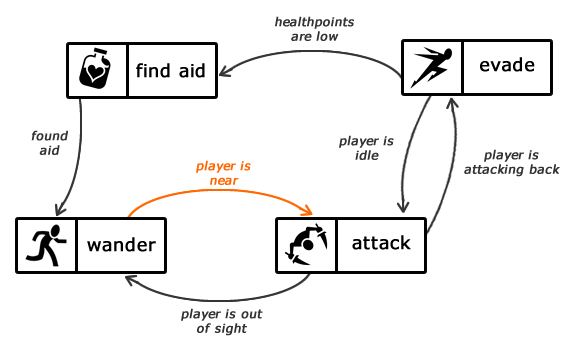
Designing the Enemy AI in your open-world game
Or Planning out your fanfic plot…

Now that we know that state machines is the hammer that we ought to use on every programming nail(xD), we are ready to run headfirst into situations like…

In order to avoid this, let us see where they are actually needed.
Consider a classic example. You are game testing an endless runner where you press space to jump. To your surprise, when you did not lift your finger from space, your character kept jumping infinitely until it exited the map and you were in the void.
This glitch occurred because the programmer coded the logic using a simple
1
2
if(keystroke == space)
character.y_coordinate += 10
This did not account for the fact that the jump should trigger only if the player is on the ground. While this is a simple example and can be easily prevented while visualising the program, it becomes obvious when formulated as a state machine.
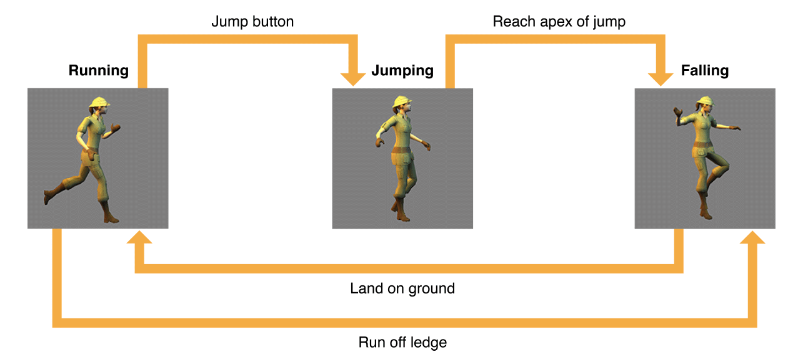
Source: GameplayKit Programming Guide: State Machines
Thus a simple abstraction into states has ensured that the game engine does not violate Newton’s third law and you can now jump only from the ground.
As your program becomes more and more complex, it is better to separate your code into states and “listen” for a valid input that would cause a transition from the current state.
Mathematical Definition
Mathematically, a deterministic finite state machine or a deterministic finite automaton is a quintuple

Well that’s scary, let us unpack the tuple
-
$\Sigma$ is the input alphabet (a finite nonempty set of symbols).
-
$S$ is a finite nonempty set of states.
-
$s_0$ is the start (or initial) state, an element of $S$.
-
$\delta$ is the state transition function; $\delta : S \times \Sigma \to S$
-
$F$ is the set of final (or accepting) states, a (possibly empty) subset of s.
While Greek’s still scary, that is still the convention. Let’s try to understand these terms better with a few examples
Revisiting the Jump example
In our jumping example, $\Sigma$ is all possible keystrokes that can be inputted and are parsed by the game. $S$ consists of the states $Running, \ Jumping, \ and \ Falling$. $s_0$ is Running. $\delta$ is illustrated in the figure. The entries of $\delta$ would look like $\delta (Running, space) = Jumping$.
Since we are not presently discussing the termination of the game, we don’t have a final state and $F = \phi$.
Thus, a deterministic finite automaton(DFA) is a mathematical model of a machine that accepts a particular set of words $F$ over some alphabet $\Sigma$. In other words, each input would represent a transition from the current state to some other state, and particular states would represent the end of the game. It is also called an acceptor as the game terminates on accepting a valid sequence(or a word) of inputs(made up of the elements of the alphabet $\Sigma$). An invalid sequence won’t terminate the machine.
A state machine can be implemented in a circuit using a sequential circuit consisting of latches. Readers familiar with Digital Electronics may recollect Melay and Moore machines.
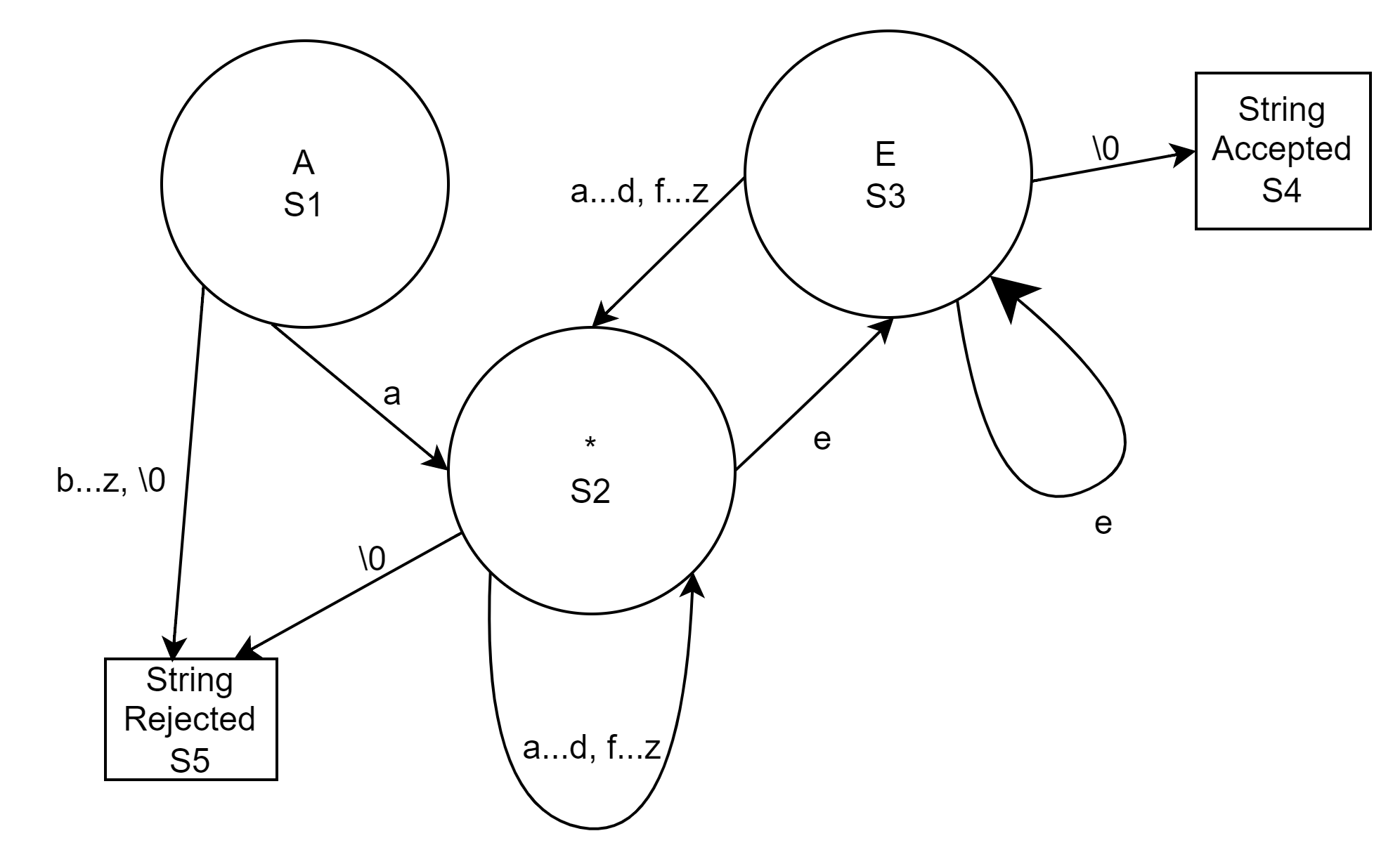
String Acceptor
In the previous section, we hinted at DFAs being acceptors. Let us see another example where this perspective becomes more obvious.
Consider a string acceptor or a regex matcher. Let us assume our regex pattern to be matched is “a*e” and our target string is “apple”.
Here, each state may represent one character in the regex pattern and the transitions represent the characters in the target string. The string is terminated by ‘\0’.

As the string “APPLE\0” is read the states followed are A(s1) -> P(s2) - > P(s2) -> L(s2) -> E(s3) -> \0(string accepted).
Here,
-
$\Sigma$ is the characters a…z, ‘\0’.
-
$S$ is states $S1$ to $S5$.
-
$so = {S1}$.
-
$\delta$ is shown in the above figure as $\delta(S1,a) = S2, \delta(S2, e) = S3, …$.
-
$F = {S4, S5}$.
Thus, a finite walk(sequence of states and state-transitions) from the source $S1$ to one of the destinations in $F$ along a word terminating with ‘\0’ signify whether the input matches the regex pattern(terminating at $S4$) or does not (terminating at $S5$).
Well, that was a mouthful

Now that we have gotten an idea of what a Finite State Machine is, look out for the upcoming post on the other classes of Automata.

Thanks for reading! I hope you’ve enjoyed reading this article. You can find me on Linkedin and GitHub.
